Mã Hóa | Câu 4 - Đề thi HSG tin 12 Nghệ An | Năm 2013-2014

Thứ năm - 11/05/2023 03:48 2.458 0

Đây là một câu khó, một bài toán số lớn (Có tới 100 chữ số). Để giải quyết bài này chúng ta cần phải dùng đến tổ hợp, kiến thức của môn toán.

Bài 4. MÃ HÓA
Nam rất thích thú với việc mã hóa các dữ liệu. Trong buổi thảo luận ở lớp Nam đã trình bày một ý tưởng rất thú vị rằng bạn ấy vừa phát minh ra một cách mã hóa mới, có thể mã các thông tin, mà không ai có thể giải mã. Cách mã hóa đó là: Với một số nguyên N, xoá các chữ số từ con số này bằng mọi cách có thể, ta sẽ nhận được các số mới. Một số cách xóa mà số mới thu được có giá trị bằng số cũ đó là khi ta xóa các chữ số 0 bên trái. Hãy tìm tổng của tất cả các con số mới thu được. Tổng này chính là mã hóa của N.
Một bạn trong lớp đã có ý kiến "Mình nghĩ cách mã hóa của cậu trên máy tính sẽ thực hiện mất nhiều thời gian với số có nhiều chữ số, chẳng hạn số có 100 chữ số. Không thể chờ để có một mã số cho số có 100 chữ số. Các mã hóa này của bạn không thể được áp dụng trên thực tế”. Nam đã trả lời "Không, không, không. Ngày mai mình sẽ đưa ra chương trình thực hiện cách mã hóa này, và sẽ mã hóa cho số có 100 chữ số trong thời gian không quá 1 giây" câu trả lời của Nam được cả lớp rất hoan nghênh. Bạn hãy giúp Nam viết chương trình đó.
Task.Yêu cầu: Cho số nguyên N (1 < N < 10¹⁰⁰) và xác định số nguyên S là mã hóa của N theo phương pháp mã hóa của Nam.
Input. Dữ liệu: Vào từ file văn bản MAHOA.INP
- Chỉ một dòng duy nhất chứa một số nguyên N. (chữ số bên trái các chữ số của NOutput. là khác 0).
Kết quả: Đưa ra file văn bản MAHOA.OUT:
- Chỉ một số duy nhất là số nguyên S tìm được.
Example. Ví dụ.

*Input.Txt* MAHOA.INP	Output.TxtNMAHOA.OUT
109 109	157 157

Giải thích test ví dụ:
N = 109. Sau khi xóa chúng ta nhận được các số:

vị trí xóa		1	2	3	1, 2	1, 3	2, 3	1, 2, 3
số mới	109	09	19	10	9	0	1	0

Tổng các số thu được: 109 + 09 + 19 + 10 + 9 + 0 + 1 + 0 = 157. Vì vậy, mã của 109 là 157.

Hướng dẫn giải.

Vì số N là số có đến 100 chữ số nên để tính kết quả cần xử lý số lớn.
Cách 1. Dùng tổ hợp xét sự xuất hiện của các số ở mỗi hàng sau đó tính tổng.
Cách 2. Sử dụng công thức. Giả sử N có dạng a₁a₂.......a_m
Kết quả là: a₁.2⁰.11^m-1 + a₂.2¹.11^m-2 + ......+ a_m.2^m-1.11⁰

Code mẫu Pascal 1

const   fi='mahoa.inp';
        fo='mahoa.out';
type    mang=array[0..201] of longint;
        bignum=record
                 d:longint;
                 cs:mang;
               end;
var     f:text;
        n,m,i,j,k,l:longint;
        s:string;
        sl,res,a,b:bignum;
procedure doc;
begin
  assign(f,fi);
  reset(f);
  readln(f,s);
  close(f);
end;
procedure nhan(a:bignum;x:longint; var t:bignum);
var n,nho,i:longint;
    c:mang;
begin
  nho:=0;n:=a.d;
  fillchar(c,sizeof(c),0);
  for i:=1 to n do
    begin
      nho:=nho+a.cs[i]*x;
      c[i]:=nho mod 10;
      nho:=nho div 10;
    end;
  if nho>0 then
    begin
      inc(n);
      c[n]:=nho;
    end;
  t.d:=n;t.cs:=c;
end;
procedure tong(a,b:bignum; var s:bignum);
var n,nho,i:longint;
    c:mang;
begin
  n:=a.d;
  if b.d>n then n:=b.d;
  nho:=0;fillchar(c,sizeof(c),0);
  for i:=1 to n do
    begin
      nho:=nho+a.cs[i]+b.cs[i];
      c[i]:=nho mod 10;
      nho:=nho div 10;
    end;
  if nho>0 then
    begin
      inc(n);
      c[n]:=nho;
    end;
  S.d:=n;S.cs:=c;
end;
procedure lam;
begin
  n:=length(s);
  sl.d:=1;sl.cs[1]:=1;
  for i:=1 to n do
    begin
      nhan(res,11,a);
      nhan(sl,ord(s[i])-48,b);
      nhan(sl,2,sl);
      tong(a,b,res);
    end;
end;
procedure ghi;
begin
  assign(f,fo);
  rewrite(f);
  with res do
    for i:=d downto 1 do write(f,cs[i]);
  close(f);
end;
begin
  doc;
  lam;
  ghi;
end.

Code mẫu Pascal 2

const fip='mahoa.inp';
      fop='mahoa.out';
type bignum=string;
var  s: string;
     kq,tong1,tong2: bignum;
     c: array[0..101,0..101] of bignum;
procedure openf;
begin
     assign(input,fip); reset(input);
     assign(output,fop); rewrite(output);
end;
function cong(a,b: bignum): bignum;
var  c: bignum;
     i,x,y,carry,sum: longint;
begin
     while length(a)<length(b) do a:='0'+a;
     while length(b)<length(a) do b:='0'+b;
     carry:=0; c:='';
     for i:=length(a) downto 1 do
     begin
          x:=ord(a[i])-48;
          y:=ord(b[i])-48;
          sum:=x+y+carry;
          carry:=sum div 10;
          c:=chr(sum mod 10 + 48) + c;
     end;
     if carry>0 then c:='1'+c;
     cong:=c;
end;
function tiny_nhan(a: bignum; b: longint): bignum;
var  p: bignum;
     i,carry,x,tich: longint;
begin
     carry:=0; p:='';
     for i:=length(a) downto 1 do
     begin
          x:=ord(a[i])-48;
          tich:=x*b+carry;
          carry:=tich div 10;
          p:=chr(tich mod 10 + 48) + p;
     end;
     if carry>0 then p:=chr(carry+48)+p;
     tiny_nhan:=p;
end;
function huge_nhan(a,b: bignum): bignum;
var  p,temp: bignum;
     i,y,j: longint;
begin
     p:='0';
     for i:=length(b) downto 1 do
     begin
          y:=ord(b[i])-48;
          temp:=tiny_nhan(a,y);
          for j:=1 to length(b)-i do temp:=temp+'0';
          p:=cong(p,temp);
     end;
     while (p[1]='0') and (length(p)>1) do delete(p,1,1);
     huge_nhan:=p;
end;
procedure init_tohop;
var  i,j: longint;
begin
     for j:=0 to 101 do c[0,j]:='1';
     for i:=0 to 101 do
          for j:=0 to 101 do if j<i then c[i,j]:='0';
     c[1,1]:='1';
     for j:=2 to 100 do
          for i:=1 to j do c[i,j]:=cong(c[i,j-1],c[i-1,j-1]);
end;
procedure xuly;
var  i,j,k,x,max: longint;
     temp1,temp2: bignum;
begin
     init_tohop;
     readln(s);
     kq:='0';
     for i:=1 to length(s) do
     begin
          tong1:='0';
          x:=ord(s[i])-48;
          max:=length(s)-i;
          for j:=0 to max do
          begin
               temp1:=tiny_nhan(c[j,max],x);
               for k:=1 to j do temp1:=temp1+'0';
               tong1:=cong(temp1,tong1);
          end;
          tong2:='0';
          for j:=1 to i-1 do
          begin
               tong2:=cong(c[j,i-1],tong2);
          end;
          tong2:=cong(tong2,'1');
          temp2:=huge_nhan(tong1,tong2);
          kq:=cong(kq,temp2);
     end;
     writeln(kq);
end;
BEGIN
     openf;
     xuly;
END.

Hai code mẫu Pascal ở trên chắc không ít bạn đọc sẽ khó hiểu, để hiểu được phần nào thì các bạn cần tìm hiểu TỔ HỢP và các xử lý cộng SỐ LƠN trong pascal.

Một số cách giải quyết bằng Python.

Cách 1: Sử dụng cách duyệt qua tất cả các số mới được tao ra. (Không tối ưu - chỉ để tham khảo)

Để giải bài tập này, bạn có thể sử dụng một vòng lặp để duyệt qua các số mới được tạo ra từ cách xóa chữ số của số nguyên a ban đầu. Sau đó, bạn có thể tính tổng của tất cả các số mới này để tìm ra mã hóa của số nguyên a. Tuy nhiên cách này không tối ưu, tôi chỉ trình bày để các bạn tham khảo. Với cách này khi duyệt qua tất cả các số mới được tạo ra thì sẽ có rất nhiều số. Ví dụ số 123, có 3 chữ số, thì khi xóa theo cách mã hóa trên thì sẽ có tới 2³ -1 = 7 số được tạo ra: 1, 2, 3, 12, 13, 23, 123. Như vậy nếu số a có 100 chữ số thì sẽ có 2¹⁰⁰ - 1 số mới được tạo ra. Do đó cách này sẽ không tối ưu bằng cách sử dụng TỔ HỢP như 2 code mẫu Pascal trên. Các bạn chỉ tham khảo thôi nhé.

with open('mahoa.inp','r') as f:
    a = f.readline().rstrip()
n = len(a) # Độ dài của a
s = 0 # Khởi tạo tổng các số mới là 0

# Duyệt qua các số mới được tạo ra từ cách xóa các chữ số của a
for i in range(1, 2**n):
    num = ''
    for j in range(n):
        if i & (1 << j):
            num += a[j]
    s += int(num)

with open('mahoa.out','w') as f:
    f.write(str(s))

Nhìn code thì các bạn cũng hiểu là không tối ưu rôi ha. Code này chỉ chạy đến test 3, sang test 4 là chạy quá 1 giây. Trong ví dụ trên chắc không ít bạn thắc mắc if i & (1 << j): Ở đây, chúng ta sử dụng biểu thức i & (1 << j) để kiểm tra xem bit thứ j của số mới i có bật hay không. Cụ thể, biểu thức này sẽ trả về một số có giá trị bằng 0 hoặc 2^j tùy thuộc vào bit thứ j của i có bật hay không. Nếu bit này bật, thì giá trị trả về sẽ là 2^j; ngược lại, nếu bit này tắt, thì giá trị trả về sẽ là 0.

Ví dụ: Nếu i = 5 (101 trong hệ nhị phân) và j = 1, thì biểu thức i & (1 << j) sẽ trả về giá trị 4 (100 trong hệ nhị phân), vì bit thứ 1 của i là 0.

Trong ví dụ của chúng ta, chúng ta sử dụng biểu thức này để kiểm tra xem chữ số nào của số nguyên a ban đầu sẽ được giữ lại trong số mới được tạo ra từ cách xóa chữ số của a.

Trong cách không tối ưu, các bạn có thể tham khảo thêm cách sử dụng hàm sau, trong hàm mình đã giải thích rồi ha:

def tao_so_moi(n, start):
    """
    Tạo số mới từ số n, bắt đầu từ vị trí start đến hết số.
    Các số mới tạo ra đưa vào danh sách new_numbers.
    """
    #Nếu số n chỉ còn lại 1 chữ số thì quay lại.
    if len(n) == 1:
        return

    #Loại bỏ tất cả các chữ số từ vị trí start và thử tìm tất cả các số mới rồi thêm chúng vào list.
    for i in range(start, len(n)):
        new_num = n[:i] + n[i+1:]
        new_numbers.append(int(new_num))
        tao_so_moi(new_num, i)

n='109'
new_numbers = [int(n)]
tao_so_moi(n, 0)
print(sum(new_numbers))

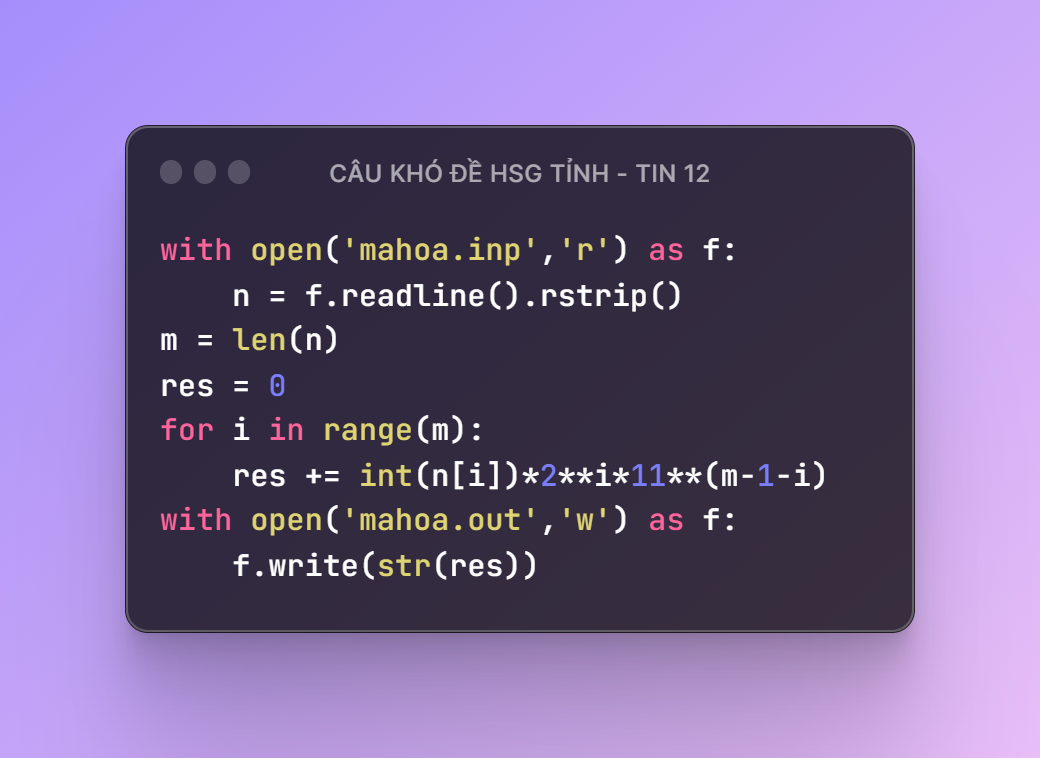
Cách 2: Sử dụng công thức toán học.

with open('mahoa.inp','r') as f:
    n = f.readline().rstrip()
m = len(n)
res = 0
for i in range(m):
    res += int(n[i])*2**i*11**(m-1-i)
with open('mahoa.out','w') as f:
    f.write(str(res))